| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Residual Connection
- Machine Learning
- Language Modeling
- Copilot
- Model Compression
- Knowledge Distillation
- Github Copilot
- 자연어처리
- GPT
- Transformer
- 딥러닝
- Pre-training
- KT
- NLP
- bert
- matrix multiplication
- Computer Vision
- AI
- ICML
- 동형암호
- 머신러닝
- Data Augmentation
- attention
- Deep learning
- Homomorphic Encryption
- Natural Language Processing
- Knowledge Tracing
- Private ML
- 표현론
- math
- Today
- Total
Anti Math Math Club
Neural Ordinary Differential Equation 본문
Neural Ordinary Differential Equation
seewoo5 2020. 11. 27. 13:18이번 포스팅에서는 2018년도 NeurIPS에서 best paper award를 받은 Neural Ordinary Differential Equation(이하 NODE, Neural ODE, ODE-Net, ODE Network)이라는 논문에 대해서 리뷰하도록 하겠습니다.
Ordinary Differential Equation(상미분방정식, ODE)란 미분 방정식 중에서 구하려는 함수가 하나의 변수에만 의존하는 경우를 말합니다. 일반적으로 다음과 같은 형태를 가집니다.

예를 들어서, 간단하면서 구체적으로 해를 구할 수 있는 경우로는 f가 z에 대한 행렬곱으로 주어지는 경우, 즉

인 경우이고 이때 해는

로 주어집니다. (행렬의 지수에 관해서는 위키피디아를 참고하시길 바랍니다.)
ODE는 왜 갑자기 나오는걸까요? NODE가 나오게 된 배경을 설명하기 위해서 일단 ResNet과 RNN이 어떻게 생겼었는지부터 짚고 넘어가도록 합시다. 먼저, ResNet은 y = x + F(x)라는 꼴을 가지고 input을 더해주는 것은 gradient vanishing problem을 해결하고 모델의 성능 역시 높이는 등의 이점을 가집니다. 이제 여러개의 residual layer를 쌓은 모델을 생각해보면 t = 1, 2, ..., T개의 layer가 있을 때 t번째 layer의 output h_t는

라는 식을 만족합니다.
이제 RNN으로 넘어갑시다. 가장 기본적인 RNN은 아래와 같이 생겼습니다.

이때 모델의 식은

로 주어지고, 여기서 g_1과 g_2는 각각 activation function을, x_t는 input, a_t는 hidden state, y_t는 output을 의미합니다. 이 식을 다음과 같이 고쳐서 쓸 수 있습니다. 이제 music generation같은 autoregressive하게 RNN을 사용하는 상황을 생각해보면, y_t = x_{t+1}이 되고, 이 경우 위의 식을 아래와 같이 다시 쓸 수 있습니다.


이렇게 쓰고 나면 위에서 쓴 ResNet을 나타내는 식과 매우 비슷하게 생겼습니다.
여기서 저자들이 떠올린 것은, 이렇게 생긴 식이 ODE를 풀 때 사용되는 Euler method와 매우 비슷하게 생겼다는 것입니다. Euler method란 ODE를 수치적으로 푸는 가장 기본적인 방법으로, fixed time interval만큼 한걸음 한걸음 풀어가는 방법입니다. (아래 그림이 Euler method를 가장 잘 나타내고 있습니다.) 이 interval의 길이를 짧게 하면 할수록 실제 ODE의 해에 좀 더 가까운 근사해를 구할 수 있게 됩니다.

위의 ResNet의 식(1)에서 layer를 좀 더 촘촘하게 만든다고 가정하고 극한으로 보내는 상황을 상상했을 때, layer가 discrete하지 않고 continuous하게 되어 있으면서 hidden state가 neural network을 정의하는 함수에 의해서 결정되는 ODE를 만족하는 무언가를 얻게 됩니다. 다시 말해서, t번째 layer(여기서 t는 0, 1, 2, 3, ...의 자연수가 아닌 0.7, 3.14등의 실수값을 가집니다.)의 output h_t는

라는 ODE를 만족하는 것 입니다. 일반적으로 F라는 함수가 좋은 조건들 (ex. Lipschitz)등을 만족할 경우 초기조건(ex. t=0일때의 값)이 주어진 ODE의 해는 유일하다는 것이 알려져 있기 때문에 위의 ODE를 풀 수만 있다면 h_1, h_3.14등의 값을 구할 수 있게 됩니다. 이는 각각 1번째, 3.14번째 layer에 대한 output같은게 되는거구요.
이렇게 Neural ODE, 혹은 ODE Network를 정의할 수 있는데, 여기서 드는 의문이 여러가지가 있습니다.
1) 이런걸 만들어서 어디다가 쓸까요? Continuous한 ResNet이 뭐가 좋을까요?
2) 위와 같이 ODE Network를 만들면, inference는 미분방정식을 풀어서 할 수 있다고 칩시다. 그러면 Backprop, 즉 모델의 parameter update는 어떻게 해야 하는 걸까요?
위의 질문들에 대한 저자들의 답은 다음과 같습니다.
1. Neural ODE의 쓰임새 및 장점
먼저, Neural ODE의 backprop에 대해서는 잠깐 뒤로 미뤄두고, 일단 만들었고 잘 돌아간다고 가정합시다. 이걸로 뭘 할수 있을까요? 일단 ResNet의 연속적인 변형이니 기존 ResNet처럼 이미지 분류에 사용할 수 있어야 될 것 같습니다. 저자들은 MNIST data에 대해서 실험을 하는데, 위의 ODE에서 F를 단순히 기존 ResNet의 CNN layer를 약간 변형해서 사용했습니다. Github에 있는 official code에 따르면, 다음과 같이 F(t, x)를 정의했습니다.
class ODEfunc(nn.Module):
def __init__(self, dim):
super(ODEfunc, self).__init__()
self.norm1 = norm(dim)
self.relu = nn.ReLU(inplace=True)
self.conv1 = ConcatConv2d(dim, dim, 3, 1, 1)
self.norm2 = norm(dim)
self.conv2 = ConcatConv2d(dim, dim, 3, 1, 1)
self.norm3 = norm(dim)
self.nfe = 0
def forward(self, t, x):
self.nfe += 1
out = self.norm1(x)
out = self.relu(out)
out = self.conv1(t, out)
out = self.norm2(out)
out = self.relu(out)
out = self.conv2(t, out)
out = self.norm3(out)
return out여기서 norm은 Group Normalization, ConcatConv2D는 t와 out을 concat한 것에 2d CNN을 적용하는 layer입니다.
def norm(dim):
return nn.GroupNorm(min(32, dim), dim)
class ConcatConv2d(nn.Module):
def __init__(self, dim_in, dim_out, ksize=3, stride=1, padding=0, dilation=1, groups=1, bias=True, transpose=False):
super(ConcatConv2d, self).__init__()
module = nn.ConvTranspose2d if transpose else nn.Conv2d
self._layer = module(
dim_in + 1, dim_out, kernel_size=ksize, stride=stride, padding=padding, dilation=dilation, groups=groups,
bias=bias
)
def forward(self, t, x):
tt = torch.ones_like(x[:, :1, :, :]) * t
ttx = torch.cat([tt, x], 1)
return self._layer(ttx)이렇게 정의된 F(t, x)에 대해서 ODE의 해가 어떻게 생겼을지는 감이 오지 않습니다. 하지만, 우리는 ODE를 풀어주는 ODE Solver가 있다고 가정할 것 입니다. (실제로 위에서 언급한 github repo에서는 Pytorch를 이용해서 ODE를 수치적으로 풀 때 가장 많이 사용되는 Runge-Kutta method등을 구현해서 사용하고 있습니다.) 그러면 embedding layer를 거친 input을 t=0일때의 initial condition이라고 가정하면 t=1일때의 output을 ODE Solver를 통해서 구할 수 있고, 이 output을 classification layer에 통과시켜서 최종적으로 prediction을 할 수 있는 모델을 만들게 됩니다.

위의 표는 실제 실험 결과를 보여주고, 여기서 ResNet은 6개의 layer를 사용했습니다. 결과에서 볼 수 있듯이 ResNet과 거의 비슷한 성능올 보여줍니다. 그런데, memory를 보면 O(1)으로 가장 작은 것을 알 수 있습니다. (L은 ResNet의 layer의 갯수입니다.) 이는 ResNet은 각 layer마다 activation을 다 저장해야 나중에 backprop을 할 수 있는 반면에, ODE Network는 그렇지 않아도 되기 때문입니다. 또한, RK-Net은 ODE-Net과 동일하지만 backprop을 할 때 Runge-Kutta method로 output을 구했던 연산을 그대로 따라서 backprop을 한 것이고, 그렇기 때문에 역시 각각의 activation들을 저장해야 합니다. (L tilde는 RK method에서 필요한 연산의 숫자입니다. ODE를 더 정확하게 풀면 풀수록 좀 더 많은 계산을 필요로 하는데, Euler method에서 step size가 작아질수록 연산 숫자가 늘어나는 것과 같은 원리입니다. ) 그렇다면 ODE-Net에서 backprop을 하는 방법이 무엇이길래 필요한 memory가 O(1)일까요? 이에 대해서는 다음 section에서 알아봅시다.
이미지 분류 이외에도 (irregular) time series data를 다룰 때 사용할 수도 있습니다. NODE의 t variable을 실제 time variable로 보는 것 입니다. 논문에서는 RNN을 encoder로, NODE를 decoder로 가지는 VAE를 만든 뒤 이를 이용해서 generative model을 만들었습니다. 실험은 spiral 모양의 해를 가지는 간단한 ODE를 만든 뒤, 이 ODE의 초기 timestamp에서의 몇개의 값을 바탕으로 이후의 값을 예측하는 task를 풀었고, discrete하게 모델링을 하는 RNN에 비해서 RMSE값이 더 작은 것을 확인하였습니다.


2. Backpropagation of ODE-Net: Adjoint method
Neural ODE에서 model parameter를 update할 때 backpropagation을 어떻게 할까요? ODE Solver가 주어졌다는 가정 하에 (저자들은 실제로 pytorch기반으로 ODE solver를 구현하였고 코드는 torchdiffeq라는 라이브러리를 참고하시면 됩니다) NODE의 inference는 ODE solver 자체의 계산으로 주어지고, 이 계산을 따라서 backprop을 할 수 있습니다. 하지만, 이보다 효율적인 방법이 있는데, 바로 adjoint method입니다. 결국에 우리가 계산하고 싶은 것은 주어진 loss L과 model parameter \theta에 대해서 gradient dL / d\theta를 계산하고 싶은 것인데, adjoint method는 이를 계산하기 위해서 새로운 ODE를 설정한 뒤 이를 t에 대해서 거꾸로 푸는 방식으로 구하게 됩니다. 이때 adjoint란 Loss를 t-step에서의 hidden state output으로 미분한

로 정의되고, adjoint는 아래의 ODE를 만족합니다.
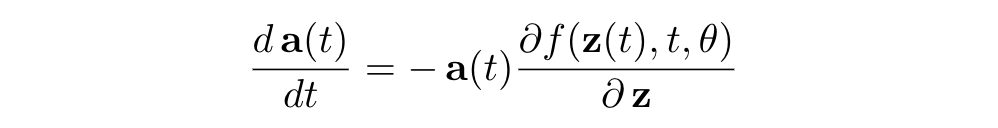
(여기서 adjoint는 row vector입니다.) adjoint를 이용하면 우리가 원래 구하고자 했던 parameter에 대한 gradient dL / d\theta를 다음과 같이 나타낼 수 있습니다.

다시말해서, parameter에 대한 gradient 역시 adjoint가 포함되어있는 새로운 ODE로부터 구할 수 있게 됩니다. 이를 바탕으로 ODE Solver를 통한 backprop을 정리하면 아래와 같습니다.

따라서, forward할 때의 ODE Solver의 계산을 따라서 backprop을 할 필요가 없이 또다른 ODE를 풀어내는 방법으로 한번에 backprop을 할 수 있기 때문에 메모리와 시간을 모두 save할 수 있게 됩니다. 특히, 메모리의 경우 discrete한 ResNet은 각 layer의 activation을 모두 저장하고 있어야 backprop이 가능한 반면, NODE는 그럴 필요가 없기 때문에 필요한 메모리가 O(1)이 됩니다.
정리하자면, ResNet과 RNN의 형태에서 영감을 받아서 ODE를 이용한 새로운 neural network를 제안했다는 것에 큰 의미가 있다고 생각합니다. 이후에 stochastic differential equation을 이용하거나 NODE와 RNN, 혹은 Transformer를 결합하는 여러가지 재미있는 후속 연구들이 있는데 이에 관해서는 읽어보시면 재밌을 것 같습니다.




