| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Homomorphic Encryption
- Pre-training
- Language Modeling
- math
- bert
- Computer Vision
- Copilot
- Model Compression
- Data Augmentation
- 머신러닝
- Transformer
- Knowledge Tracing
- Natural Language Processing
- Knowledge Distillation
- 자연어처리
- KT
- 동형암호
- Residual Connection
- GPT
- Github Copilot
- Deep learning
- Machine Learning
- NLP
- attention
- ICML
- AI
- 딥러닝
- matrix multiplication
- 표현론
- Private ML
- Today
- Total
Anti Math Math Club
Constructions in combinatorics via neural networks 본문
Constructions in combinatorics via neural networks
seewoo5 2021. 5. 2. 14:22이번에는 기존에 이 블로그에서 리뷰하던 대부분의 딥러닝 논문들과는 성격이 좀 다르지만 굉장히 흥미로운 결과를 담고 있는 논문을 리뷰하고자 합니다. 저는 지금은 인공지능 관련 일을 하고 있지만 본업은 수학이며 학위를 진행중인 상태입니다. 그래서인지 인공지능 공부를 하면서 가장 궁금했던것은 인공지능이 정말로 논리적인 '사고'라는것을 할 수 있는지, 특히 수학적인 명제에 대한 '증명'을 스스로 할 수 있는지에 대해서 의문을 자주 가졌습니다. 예전에는 정말 머나먼 이야기라고 생각했지만, 요즘에는 생각이 조금씩 바뀌고 있습니다. 최근에 Lean이라는 언어를 이용해 수학의 매우 기본적인 공리들부터 시작해서 최신 이론들까지 컴퓨터로 formalize하려는 시도가 여러 사람들에 의해서 이루어지고 있고, 이 프로젝트의 궁극적인 1차 목표는 수학 올림피아드 문제를 formal한 형태로 입력을 받아서 그 증명을 출력할 수 있는 AI를 만드는 것이라고 합니다. (링크) 물론 아직은 멀었지만, 좀 더 많은 부분이 formalize되고 (이미 기본적인 학부 수학들 대부분은 Lean으로 작성되었다고 합니다) 여기에 자연어 처리 모델들을 잘 활용한다면 곧 수학 증명을 하는 AI도 나오지 않을까.. 하는 생각이 듭니다.
이번에 소개할 Constructions in combinatorics via neural networks라는 논문은 실제로 딥러닝 모델이 의미있는 수학적인 결과를 낼 수 있다는것을 보여준 논문입니다. 논문의 내용을 요약하자면, 강화학습을 이용해서 조합론, 특히 그래프 이론의 몇몇 추측들에 대한 반례를 찾아낼 수 있다는 것을 보였습니다. 좀 더 자세히 말하자면, 단순한 MLP를 policy network로 두고 cross-entropy method를 이용해서 몇몇 그래프 관련 추측들에 대한 반례들을 발견했는데, 디테일을 알기에 앞서서 먼저 강화학습의 기본적인 개념과 cross-encropy method가 무엇인지부터 알아봅시다.
강화학습은 잘 알려진 알파고(AlphaGo)를 만드는데에 사용된 머신러닝 방법론으로써, 특정 모델(agent)이 특정 행동(action)을 함으로써 보상(reward)를 받는 체계 내에서 이 보상을 최대화하는 방향으로 모델을 학습시키는 것이라고 할 수 있습니다. 예를 들어, 알파고는 바둑의 현재 돌이 놓여있는 상태(state)에서 특정 지점에 돌을 놓았을 때의 이길 확률을 구하고, 이를 바탕으로 가장 확률이 높은 곳에 돌을 두게 되며, 이렇게 게임을 진행했을 때의 승/패를 바탕으로 모델을 업데이트하게 됩니다. 강화학습에는 여러가지 알고리즘들이 있는데, 이 알고리즘들은 다음과 같이 분리할 수 있습니다.
- model-based vs model-free: 강화학습에서의 환경(environment)는 각 상태에서 특정 행동을 했을 때 상태가 어떻게 바뀌는지 결정하는 것이라고 보면 됩니다. 만약 환경에 대한 model이 있다면 model-based라고 하고, 그렇지 않다면 model-free라고 합니다.
- value-based vs policy-based: value란 보통 미래에 받게 될 보상의 총합으로 정의되고, policy는 각 state마다 어떤 action을 취할지를 결정하는 함수라고 볼 수 있습니다. value-based method란 value function만을 학습함으로써 자연스럽게 policy는 value를 최대화하는 action을 선택하는 방법을 말하고, policy-based method는 따로 value function을 학습하지 않고 오로지 policy만을 학습하는 방법을 의미합니다. (value와 policy에 대한 model을 둘 다 사용하는 actor-critic과 같은 알고리즘도 있긴 합니다.)
이 중에서 cross-entropy method는 model-free이면서 policy-based인 알고리즘에 속합니다. cross-entropy method의 알고리즘은 다음과 같습니다.
- 지금의 policy network(model)을 바탕으로 N개의 episode를 진행합니다. 이때 policy network의 output을 바탕으로 sampling을 하는 Monte Carlo 방법을 이용합니다.
- 그 중에서 return이 가장 큰 일부 episode만 남기고 나머지는 버립니다.
- 남은 episode의 action을 label로, state를 input으로 생각해서 policy network를 학습시킵니다.
이를 반복하게 되면, 결국에는 policy network가 return이 높아지도록 하는 policy를 학습하게 된다는 원리입니다. Cross-entropy method는 간단하고 구현도 어렵지 않으며 value-based인 방법들에 비해서 hyperparameter에 덜 민감하고 수렴이 잘 된다는 장점을 가지고 있지만, environment가 복잡한 경우에는 사용하기 어렵다고 합니다.
그렇다면 cross-entropy method를 이용해서 어떤 문제를 풀어낸걸까요? 이 논문에서는 그래프 이론 문제 말고도 312-pattern avoiding 0-1 matrix의 permant의 최댓값의 lower bound를 찾는다거나 hypercube의 부분집합을 몇개의 평면으로 덮을 수 있는지에 대한 exact covering 문제 등 다양한 조합론 문제에 대한 접근을 제시하지만, 이 글에서는 그래프 이론에 대한 문제의 반례를 찾는 과정에 대해서만 소개하도록 하겠습니다. (참고로 뒤에 있는 몇몇 반례들은 cross-entropy method가 아닌 linear programming을 이용합니다.)
첫번째 conjecture는 그래프의 spectrum과 matching number, 그리고 vertex의 갯수에 대한 부등식으로, 다음과 같습니다.

용어들에 대해서 설명하자면, 그래프의 eigenvalue란 그래프의 Laplacian matrix의 eigenvalue를 말하는데, 여기서 laplacian matrix는 그래프의 인접행렬(adjacency matrix) A와 차수행렬(degree matrix, 대각성분이 각 vertex의 degree인 행렬) D의 차이인 L = D - A로 정의되고, 이 행렬은(특히 eigenvalue는) 그래프의 엄청나게 많은 성질들을 담고 있음이 알려져있고, 이를 연구하는 분야가 바로 spectral graph theory입니다(예를 들어, largest eigenvalue의 값이 2인것과 그래프의 각 connected component가 nontrivial bipartite graph라는것이 동치임이 알려져 있습니다). Matching number는 주어진 graph의 subgraph중에서 각 vertex의 degree가 1 이하인, 즉 모든 edge가 서로 인접하지 않는 subgraph(matching이라고 부릅니다)의 edge 갯수 중 최댓값을 의미합니다. 이름 그대로 맺을 수 있는 짝의 최댓값 정도로 생각하면 될 것 같습니다. 위의 부등식은 임의의 연결그래프의 가장 큰 eigenvalue와 matching number의 합이 항상 sqrt(n-1) + 1 이상이라는 것인데, 이 논문의 저자는 이에 대한 반례를 바로 위에서 언급한 cross-entropy method를 이용해서 찾아냅니다. 자세한 과정은 다음과 같습니다.
먼저, 그래프 자체를 모델의 input으로 넣어줘야 하는데, 총 가능한 nC2 = n(n-1)/2개의 edge중 어떤게 연결되어있고 어떤게 연결되어 있지 않은지를 길이 nC2의 binary sequence로 표현해서 그래프를 나타냅니다. 그 다음, 아직 미완성인 그래프를 state로 생각하고 이를 policy network에 넣어주게 되면 network의 output은 그 다음 index에 해당하는 edge를 추가할 확률을 return합니다. 그러면 이 확률값을 바탕으로 sampling을 해서 그 다음 edge를 추가할지 안할지를 결정하고, 이를 모든 nC2개의 edge에 대해서 차례대로 수행합니다. (마치 GPT와 같은 causal language modeling과 비슷하다고 할 수 있습니다.) 이렇게 모든 edge에 대해서 생성을 완료하면 vertex n개짜리 그래프가 나오고 이 그래프(=episode)에 대해서 reward(여기서는 return과 같습니다)를 다음과 같이 계산합니다.

이 reward식을 자세히 보면 위의 부등식을 "뒤집은"것에 불과한데, 이 값이 항상 0 이하라는것이 위의 추측이며 우리는 policy network이 이 reward값을 최대화하도록 학습이 되다 보면 언젠가는 0보다 큰 G를 생성해내지 않을까 하는 믿음으로 cross-entropy method를 사용하게 됩니다. 이를 요약하자면 아래 그림과 같습니다. (NN이 policy network에 해당합니다)

실제로 실험에서는 n=19일때 이 방법을 찾아냈는데, 아래 그래프를 보면 실제로 학습이 진행됨에 따라서 reward가 변화하고, 결국 충분한 step이 지나면 원하는 반례가 찾아지게 됩니다. (아래 그래프는 reward가 증가하는게 아닌 감소하는 형태로 되어있고 식도 다른데, 실제 github에 있는 구현을 보면 위에서 언급한대로 reward를 정의하고 훈련을 시킨것으로 보입니다. 결국 같은 이야기를 하는것이니 방향은 크게 중요하지 않긴 합니다.)

아래의 그림은 iteration이 지날수록 변화하는 그래프의 모습을 나타낸 것인데, 처음에는 매우 random한 형태의 그래프로 시작했다가 점점 특정한 구조를 가지게 되면서 결국 마지막에는 "balanced double star"라고 부를 수 있는, 두개의 star graph가 연결된 형태로 수렴하는것을 알 수 있습니다. 사실, 위의 conjecture 2.1은 이미 이 논문에서 반례가 제시되었는데, 논문의 반례는 vertex가 600개인 그래프라는 점에서 neural network가 훨씬 더 작은 반례를 찾아낼 수 있었다는것에 의의가 있습니다.

이 논문에서 반증한 또 하나의 conjecture는 그래프의 proximity와 distance spectrum에 관한 부등식으로, 아래와 같습니다.

여기에 나오는 용어를 설명하자면, proximity란 그래프 위의 각 vertex들로부터 다른 vertex들 까지의 거리의 평균 중에서 가장 짧은 값을 의미하고, 아래와 같이 정의됩니다.
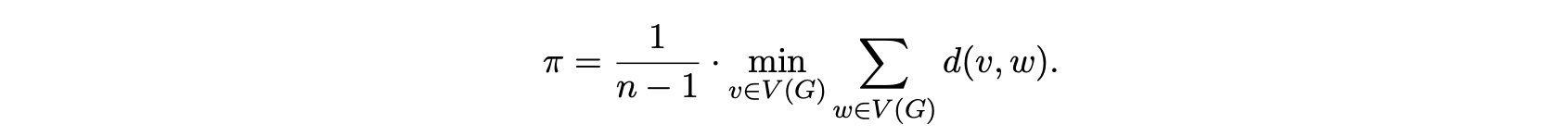
그래프의 edge가 많을수록, 즉 서로 많이 연결되어있을수록 이 값이 줄어들게 됩니다. Distance spectrum은 laplacian spectrum과 비슷하게 distance matrix의 eigenvalue를 의미하며, distance matrix는 (i, j)성분이 i번째와 j번째 vertex사이의 거리가 되는 행렬을 말합니다. proximity와 distance spectrum 사이에는

가 성립하는 것이 이미 알려져있는데, 위의 conjecture는 이보다 조금 더 강한 버전의 추측이라고 할 수 있습니다. 하지만 이 역시 위에서 이야기한 방법과 거의 같은 방법으로 반례를 찾을 수 있었고, 여기서 차이점은 reward function만 이 부등식에 대응되는

로 두고 학습을 합니다. 하지만 안타깝게도, computational resource의 한계로 인해서 n<=30까지만 실험을 했는데, 이 크기로는 반례가 찾아지지 않았습니다. 다만, n=30일때 학습이 많이 진행될수록 다음과 같은 형태의 그래프로 점점 수렴했다고 합니다.

위의 실험이 알려주는것은 만약 반례가 존재한다면 위와 같이 꼬리가 두개 달린 혜성같은 모양(실제로 double-tailed commet이라고 부른다고 합니다)을 띄지 않을까 하는 힌트를 제공하고, 결론적으로 아래와 같은 반례를(여기서는 컴퓨터가 아닌 손으로) 찾아냈다고 합니다. 결국에는 conjecture 2.1과 같이 직접적으로 반례를 찾아낸 것이 아니더라도, 반례를 찾는 데에 있어서 굉장히 큰 힌트를 제공했다는 것을 알 수 있습니다.

이 외에도 논문에는 distance matrix와 adjacency matrix의 characteristic polynomial의 계수의 peak이 멀리 떨어질 수 있다거나, transmission regularity가 distance spectrum으로 결정되지 않는다는 등의 반례들을 추가적으로 제시하지만, 여기서는 따로 언급하지 않도록 하겠습니다. 제 감상평으로는 논문의 아이디어 자체가 매우 간단하면서도 실제로 딥러닝으로 어느정도 의미있는 수학적인 발견을 해낼 수 있다는 가능성을 처음으로(?) 제시했다는 점에서 시사하는 바가 매우 크다고 생각합니다. 사실 수학적인 결과를 머신러닝으로 찾아낸건 2019년에 나온 Ramanujan machine이라는게 이미 있었긴 하지만, 개인적으로는 이 논문의 결과가 좀 더 마음에 듭니다. 다만 논문에서 반례를 제시한 많은 conjecture(였던것)들이 그렇게 잘 알려진 문제들은 아니었기에, 좀 더 많은 수학자들이 관심을 가지는 문제에 대해서 반례를 찾아내거나 혹은 증명을 할 수 있는 아이디어를 제공할 수 있다면 좀 더 임팩트가 크지 않을까 싶습니다.




