| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Machine Learning
- Github Copilot
- 딥러닝
- math
- Data Augmentation
- Pre-training
- AI
- Homomorphic Encryption
- KT
- Model Compression
- bert
- 표현론
- 자연어처리
- Deep learning
- attention
- Language Modeling
- matrix multiplication
- GPT
- Computer Vision
- NLP
- 머신러닝
- Knowledge Tracing
- Residual Connection
- Private ML
- Knowledge Distillation
- Copilot
- Transformer
- 동형암호
- Natural Language Processing
- ICML
- Today
- Total
Anti Math Math Club
Advancing mathematics by guiding human intuition with AI 본문
Advancing mathematics by guiding human intuition with AI
seewoo5 2022. 1. 27. 12:10저번 포스팅에서는 Copilot을 이용해서 학부 수준의 수학 문제를 푸는 AI에 대해서 소개를 했습니다. 이번에는 AI가 실제로 학부 수준을 넘어선, 연구 수준의 문제를 푸는 데에 도움을 준 케이스에 대해서 이야기하고자 합니다. (저번처럼 문제를 푼게 아니라, 푸는데에 도움을 주었다는것이 중요합니다. 제 생각에는 실제로 연구 수준의 증명을 생성하는 AI가 나오려면 최소 10년은 더 있어야 할 것 같습니다.)
보통 사람들이 생각하는 AI는 스스로 생각하고 걸어다니고(?) 사람을 지배하는(??)걸 떠올리는 경우가 많은데, 실상은 몇년 전까지만 해도 강아지와 고양이 사진을 잘 분류해내는 숫자 덩어리에 불과했습니다. 이제는 고화질의 이미지와 비디오를 만들어내고 번역도 하고 글도 쓰고 작곡도 하고... 할 수 있는 일이 눈에 띄게 많아졌습니다. 하지만 AGI, 즉 Artificial General Intelligence를 만들었다고 하기에는 아직 부족한 감이 있는데요, 정말 AI가 사람처럼 사고를 할 수 있는지를 확인하기 위해서 개인적으로는 수학을 물어보는 것 만큼 좋은게 없다고 생각합니다. 물론 제대로 답을 한다고 해서 정말로 사고를 한다고 볼 수 있을지는 모르겠지만요.
앞에서도 말씀드렸지만 AI로 연구 수준의 수학 문제를 풀어내는건 아직 머나먼 이야기라는 생각이 듭니다. 다만 연구에 도움이 되는 경우는 생각해 볼 수 있겠죠. 이전에 소개한 논문이 딱 좋은 예시 중 하나인데, 그래프 이론의 몇몇 추측에 대한 반례를 강화학습을 통해서 찾아냈습니다. 하지만 증명을 도와준게 아니라 오히려 반례를 찾아냈다는 점에서는... 문제를 풀어낸 건 맞지만 약간 아쉬운(?) 감이 있습니다.
이번에 소개하고자 하는 연구는 DeepMind에서 얼마 전에 Nature에 발표한 결과로, 실제로 순수 수학 문제를 풀어내는데에 AI가 어느정도 도움을 주었다는 흥미로운 내용을 담고 있습니다. 아이디어 자체는 어렵지 않은데, 수학자가 생각하는 직관을 ML 모델을 이용해서 supervised learning으로 한번 테스트를 해보자는 것 입니다. 예를 들어서, 다면체의 면의 갯수와 다면체의 다른 성질들, 즉 꼭짓점의 갯수, 변의 갯수, 넓이, 부피 등이 어떤 관련이 있을지를 알아보기 위해 4개의 feature (꼭짓점의 갯수, 변의 갯수, 넓이 부피)를 입력으로 받아서 면의 갯수를 출력하는 함수를 학습을 해보는 것 입니다. 이때 학습에 필요한 데이터를 만드는건 다면체를 임의로 많이 만들고 각각에 대한 숫자만 뽑아내면 되니까 어렵지 않은 편이죠 (넓이나 부피같은게 좀 까다롭긴 하겠지만...) 이 경우 오일러의 공식 v - e + f = 2에 의해서 우리는 학습하고자 하는 함수가 y = (1, -1, 0, 0) * X + 2가 될 것이라는걸 알고 있고, 이 경우에는 모델만 잘 고르면 쉽게 학습이 될 것이라고 예측할 수 있습니다. 하지만, 실제 연구에서 푸는 문제는 이보다 훨씬 어렵고 복잡하며, 심지어는 무슨 문제를 풀어야하는지조차 모르는 경우도 많습니다. 이 논문의 요지는 연구 수준의 수학문제 역시 ML이 어느정도 가이드를 주는게 가능하다는 것이고, 이와 관련해서 크게 두가지의 예시를 제공합니다. 하나는 매듭이론(Knot Theory)에 대한 결과이고, 또 하나는 표현론(Representation Theory)에 대한 결과인데, 제가 아는 선에서 최대한 자세히 소개를 해보고자 합니다.

1. 매듭이론 (Knot Theory)
매듭이란 무엇일까요? 매듭이라는 말을 들었을 때 상상되는 그 이미지, 그게 바로 매듭입니다. 수학적으로는 3차원 공간 안에 정의된 단순폐곡선(겹치는 부분이 없는 곡선)으로 정의가 되고, 그 종류는 무수히 많습니다. 당장 우리한테 신발끈을 던져주면서 맘대로 매듭을 만들어보라고 하면 (신발끈이 충분히 길다는 가정 하에) 얼마든지 복잡한 매듭을 만들어낼 수 있죠. 매듭 이론을 연구하는 수학자들이 가장 관심이 있는 문제는 매듭의 분류 문제로, 세상에 있는 매듭이 어떤 것들이 있는지, 또 2개의 매듭이 주어졌을 때 이 둘이 같은지를(여기서 같다는건 매듭을 끊지 않고 이리저리 움직여서 똑같이 만들 수 있는지를 의미하고, 영어로는 isotopic하다고 합니다) 어떻게 알 수 있을지에 관심이 많고, 무수히 많은 연구 결과들이 있습니다. 예를 들어, 매듭에는 여러가지 방법으로 불변량(invariant)들을 정의할 수 있는데, 이는 계산하기 어렵지 않으면서 같은 매듭은 같은 불변량을 가질 수 밖에 없는 것들을 말합니다. 가장 간단한 불변량으로는 주어진 매듭을 평면에 그릴 때 필요한 최소 교차점부터 Jones Polynomial, Alexander Polynomial과 같은 다항식, 매듭의 여집합의 기본군(fundamental group)등, 굉장히 많은 불변량들이 있습니다. 아쉽게도 매듭을 완벽하게 분류할 수 있는, 즉 불변량이 같은 것과 매듭이 같은것이 동치가 되는 그런 꿈의 불변량은 아직 발견되지 않았습니다.
이 논문에서는 매듭의 여러 불변량들 사이의 알려지지 않은 관계를 머신러닝으로 찾아냅니다. 앞에서 언급한 framework대로, 먼저 여러 매듭들과 그 불변량들이 매듭의 signature와 무슨 관련이 있는지를 ML을 이용해서 학습을 시도해 봅니다. (Github에 있는 official 코드를 확인해보니 그냥 sigmoid를 activation으로 사용한 MLP를 사용한 것 같습니다.) 놀랍게도, 그 많은 불변량들 중에서 매듭의 쌍곡부피(hyperbolic volume)과 meridional translation, longitudinal translation이 signature를 예측하는데에 가장 중요한 feature들로써 작용함을 찾아냅니다. 이를 바탕으로 매듭의 기울기(natural slope)라는 불변량을 새로 정의하고, 다음과 같은 부등식이 성립한다는 추측을 합니다.

(여기서 sigma(K)는 signature, vol(K)는 쌍곡부피를 의미합니다.) 안타깝게도, 위의 부등식은 많은 반례들이 있었습니다. 하지만 여기서 굴하지 않고, injectivity radius라는 불변량까지 추가를 해서 다음의 수정된 부등식이 성립한다는 추측을 합니다.

그리고 놀랍게도, 이 부등식은 참이라는것을 몇몇 수학자들이 증명하는데에 성공합니다. 여기서 주목할 점은 signature는 대수적(algebraic)으로 정의된 불변량이고(정확히는 매듭의 Seitfert surface의 homology의 intersection form의 행렬의 symmetric sum의 signature로 정의를 합니다) slope나 volumn, injectivity radius등은 모두 기하학적(geometric)으로 정의된 불변량인데, 이 부등식은 지금까지 없었던 대수적인 불변량과 기하학적인 불변량 사이의 관계를 나타내는 최초의 결과라는 점 입니다. 또한, 이 부등식으로부터 얻을 수 있는 여러 따름 정리들이 있는데, 이에 대해서는 바로 위의 논문을 참고하시길 바랍니다.
2. 표현론 (Representation Theory)
표현론이란, 간단하게 말해서 행렬을 이용해서 대칭을 다루는 학문입니다. 수학에서 말하는 대칭이란 정확히는 특정한 구조가 주어져있는 집합을 의미합니다. 예를 들어 군(group)이라는 개념이 있는데, 이는 결합법칙이 성립하면서 항등원이 존재하고 임의의 원소의 역원이 (유일하게) 존재하는 이항 연산이 주어진 집합을 의미합니다. 예를 들어서, 정수들의 집합은 덧셈에 대해서 결합법칙이 성립하고, 0이라는 항등원이 존재하며, 임의의 정수 a에 대해 -a라는 역원이 존재하기 때문에 정수집합에 덧셈이라는 연산을 준 것은 군이라고 할 수 있습니다. 이 포스팅에서 다룰 대상은 대칭군이라는(군이 대칭이라고 했으니 대칭대칭이네요), S_n이라고 표기하는 군 입니다. 이는 집합으로써는 {0, 1, 2, ..., n - 1}에서 자기 자신으로 가는 일대일 대응들을 모아놓은 것이고, 이 위에 연산은 함수의 합성으로 주어집니다. 그러면 위에서 말한 군의 모든 조건을 만족하게 됩니다. S_n의 원소의 갯수는 n!개가 되겠죠?
수학자들은 어떤 군이 주어져 있으면 그 군에 대해서 갖은 방법으로 연구를 하는데, 그 중 하나가 바로 표현론입니다. 앞서 표현론이란 행렬을 이용해서 대칭, 즉 군을 다룬다고 했는데, 이는 다시 말하면 군에 있는 각 원소를 적당한 행렬에 대응시키는 것 입니다. 이때 이 대응 자체는 연산을 보존해야하는데, 좀 더 정확히 말하면 군의 두 원소 x, y가 있으면 각각에 대응되는 행렬 f(x), f(y)의 곱이 두 원소를 연산한 결과 x*y에 대응되는 행렬 f(x*y)와 일치해야 합니다. 이를 만족하는 f를 준동형사상(homomorphism)이라고 부릅니다. 그 중에서 가장 대표적인 예시가 Kazhdan-Lusztig 다항식인데, 이름에서 알 수 있듯이 Kazhdan과 Lusztig라는 수학자 두명이서 만든 다항식입니다. 정의 자체는 굉장히 복잡한데, 1) 대칭군의 임의의 두 원소 x, y에 대해 다항식 P_{x, y}(q)가 정의되고, 2) 정의 자체는 매우 복잡한 방법으로 귀납적으로 정의된다는것만 기억하시면 됩니다. 이 다항식이 S_n과 밀접한 관련이 있는 n x n 행렬들의 집합(정확히는 gl_n으로 표기되는 리대수를 말합니다)의 표현론과 깊은 관련이 있다는게 Kazhdan-Lusztig 추측이었고, 이는 Beilinson, Bernstein, Brylinski, Kashiwara라는 수학자들에 의해서 증명이 되었습니다.
그 이후로도 이 다항식에 대한 연구는 계속되었는데, 그 중에서 아직 안풀린 추측이 바로 조합불변추측(combinatorial invariance conjecture)입니다. 이 추측이 무엇인지 이야기를 하기 전에 먼저 Bruhat 그래프라는 것을 정의...는 하지 않겠습니다. 이는 대칭군의 임의의 두 원소 x, y에 대해서 정의되는 그래프로, n이 커질수록 매우 복잡해진다는것만 짚고 넘어가겠습니다. 아래는 n = 6, x = (021435), y = (234501)일때의 Bruhat 그래프와 Kazhdan-Lusztig 다항식을 나타낸 그림입니다.
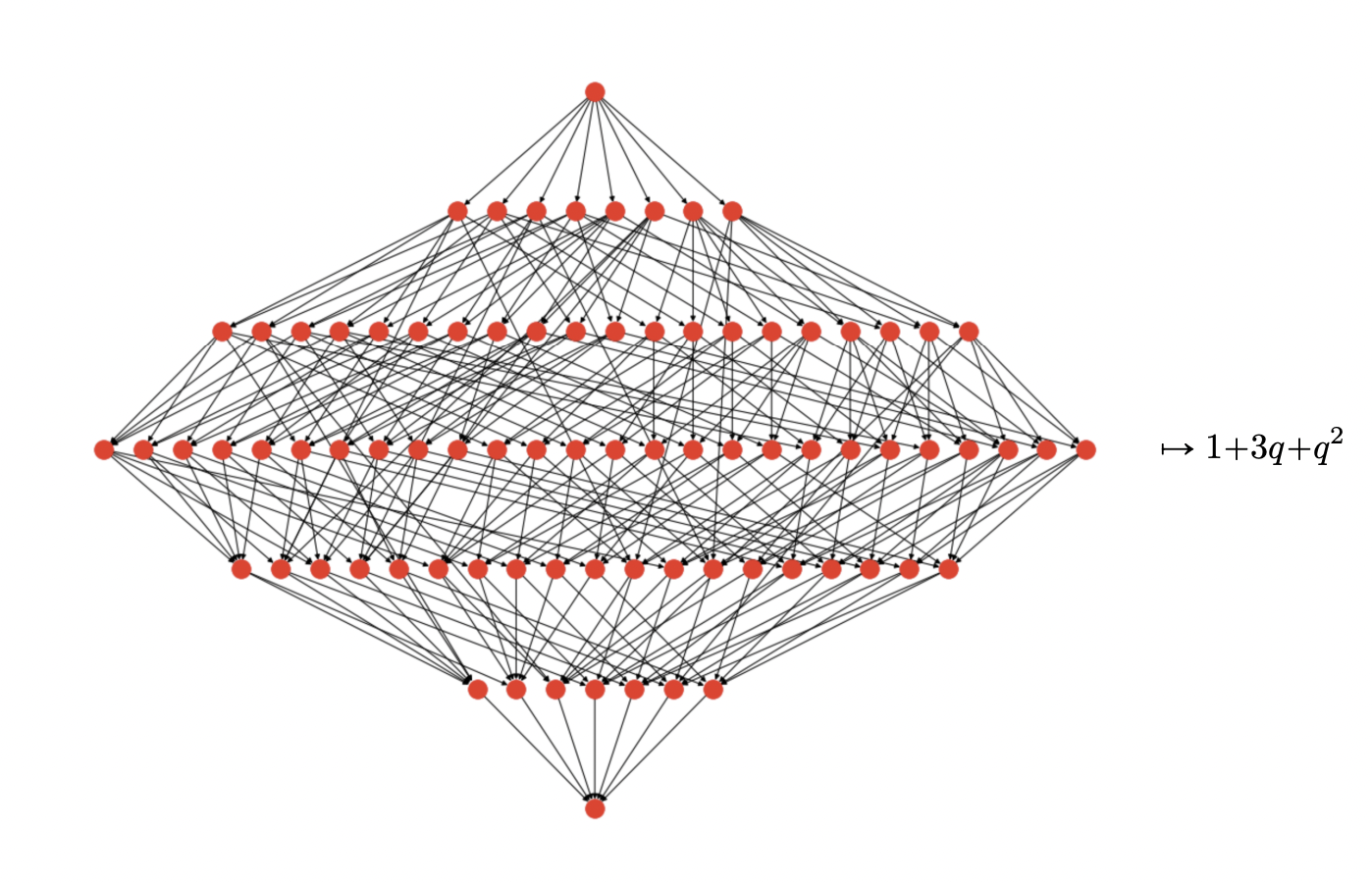
Combinatorial invariance conjecture가 주장하는것은, 왼쪽의 매우 복잡합 그래프만 가지고 오른쪽의 다항식을 얻어낼 수 있다!입니다. 다시 말해, 서로 다른 (x, y)에 대해서 Bruhat 그래프가 같아지는 경우들이 있는데, 이 때 Kazhdan-Lusztig 다항식 P_{x, y}(q)역시 똑같다는 주장이죠. 왼쪽과 같은 무지막지한 그래프에 다항식의 정보를 담고있는 어떤 숨겨진 구조가 있다는 것인데, 왜 아직까지 추측으로 남아있는지 이해가 갑니다. 하지만, 우리는 지금까지 매우 많은 사례등을 통해서 머신러닝과 딥러닝이 어떤 특정한 패턴을 찾아내는 일에는 도사라는것을 봐왔는데, 그러면 저 그래프에 대해서도 어떤 인사이트를 얻을 수 있지 않을까요? 이런 생각에서 출발해서 저자들은 Neural Message Passing for Quantum Chemistry라는 논문에서 제시한 MPNN(Message-Passing Neural Network)를 이용해서 Bruhat 그래프를 input으로, Kazhdan-Lusztig 다항식을 output으로 두고 실험을 해봅니다. 그 결과, 예측에 있어서 모델이 S_n의 특정 원소들에 크게 기대는 것을 알 수 있었고(아래 그림의 a), 이를 바탕으로 수학자들은 다음과 같은 추측을 만듭니다.
Conjecture. Every Bruhat interval admits a canonical hypercube decomposition along its extremal reflections, from which the KL polynomial is directly computable.
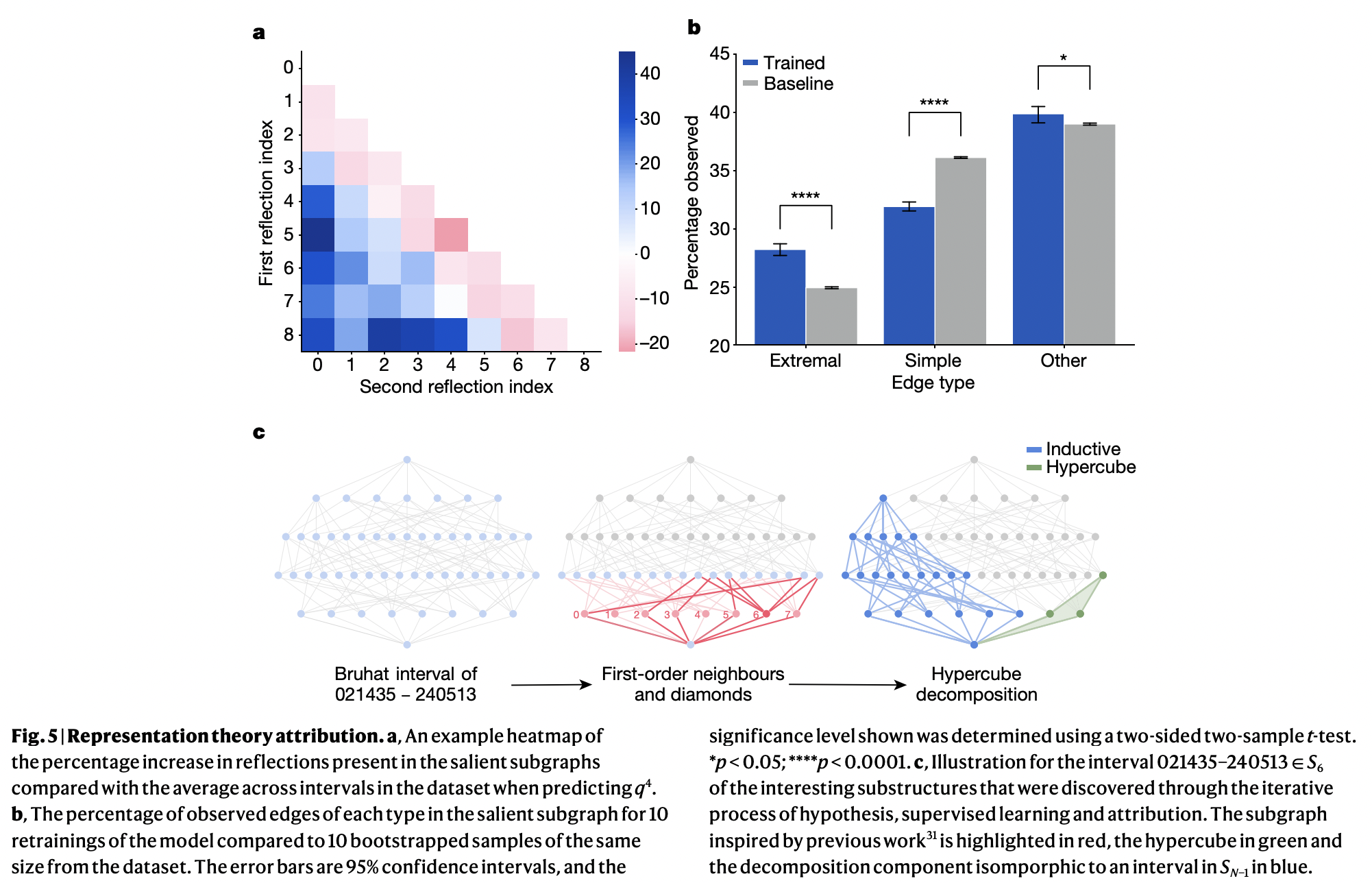
해석하자면, 임의의 S_n의 원소에 대한 Bruhat 그래프를 S_{n-1}의 원소에 대한, 더 작은 Bruhat 그래프와 hypercube 그래프로 나눌 수 있고(hypercube decomposition이라고 부릅니다), 이렇게 나누게 되면 기존의 Kazhdan-Lusztig 다항식을 더 작은 그래프들로부터 쉽게 계산해낼 수 있다는 것 입니다. 그리고 놀랍게도(2), 위의 추측이 참이라는 것을 몇몇 수학자들이 증명해냅니다. 이 결과로부터 알 수 있는것은, 만약 우리가 Bruhat 그래프를 어떻게 decompose하는지에 관계 없이 각 decomposition의 Kazhdan-Lusztig 다항식이 동일하다는것만 증명한다면, S_n에 대한 combinatorial invariance conjecture가 참임을 보일 수 있게 된다는 사실입니다. 안타깝게도 이것까지는 증명이 되지 않았지만, hypercube decomposition을 이용해서 확인해 본 결과 n이 9 이하인 경우 많은 경우에 성립한다는 것을 컴퓨터로 확인할 수 있었다고 합니다.
3. 결론
논문을 읽은 소감은, 수학을 전공하(고 있지만 잠깐 변절을 하)고 있는 사람으로써, 이런 류의 수학이 좀 더 발전했으면 좋겠다는 생각을 했습니다. 편견일 수 있지만 제 생각에는 이러한 접근을 잘못된 접근이라고 여기는 수학자가 꽤 많을 것 같은데, 저는 이제는 컴퓨터의 도움을 많이 받아서 수학을 해야 하는 시대가 왔다고 생각하고, 이 논문의 결과는 그 중에서도 가장 참된 예시를 보여준다고 생각합니다. 개인적으로는 이 논문을 읽으면서 시도를 해보고 싶은 것들이 좀 떠올라서 제 연구에도 적용을 해보고 싶습니다.




