| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Private ML
- Knowledge Distillation
- NLP
- Pre-training
- 동형암호
- Computer Vision
- bert
- 딥러닝
- 머신러닝
- Homomorphic Encryption
- 자연어처리
- Github Copilot
- Data Augmentation
- GPT
- AI
- Transformer
- Deep learning
- Natural Language Processing
- Residual Connection
- Machine Learning
- Knowledge Tracing
- math
- attention
- Model Compression
- 표현론
- Language Modeling
- ICML
- KT
- matrix multiplication
- Copilot
- Today
- Total
Anti Math Math Club
Reformer: The Efficient Transformer 본문
Reformer: The Efficient Transformer
seewoo5 2020. 5. 9. 20:35이번 포스트에서는 Google에서 올해 초에 발표하고 ICLR2020에 accept된 Reformer: The Efficient Transformer에 대해서 알아보도록 하겠습니다.
Synthesizer 리뷰에서도 언급했었지만, 2017년에 Google에서 발표한 Transformer는 NLP를 포함해서 music generation, image generation, knowledge tracing, time series prediction등 여러가지 seq2seq task에서 state-of-the-art의 성능을 보여주고 있습니다. CNN 모델들이 그렇듯이, NLP 혹은 다양한 seq2seq 문제를 해결하기 위해서 점점 더 큰 Transformer를 사용하게 되고, 최근에 Microsoft에서 발표한 DeepSpeed는 무려 17억개의 parameter를 가지고 있습니다. (물론, Microsoft에서는 이를 효율적으로 Train할 수 있는 방법을 개발했기 때문에 train을 할 수 있습니다.) 하지만, GPU 1개만 가지고 있는 개인 연구자의 경우 DeepSpeed는 커녕 BERT조차 fine-tuning하는 것이 어려울 수 있습니다.
이를 해결하기 위해서 Transformer의 time & space complexity를 줄이려는 시도를 하게 되는데, 그러기 위해서는 Transformer의 어떤 부분이 계산 시간과 메모리에 영향을 주는지를 파악해야 합니다. Reformer 논문에서는 다음의 3가지 Bottleneck을 이야기하고 있습니다.
1. 모델을 훈련시킬 때, backprop을 하기 위해서는 각 layer의 activation을 알고 있어야 합니다. 그래서 총 메모리는 layer숫자에 비례하게 됩니다. 16개의 layer를 쓰는 큰 Transformer 모델(BERT 등)의 경우에는 1개의 layer를 쓸 때보다 약 16배의 메모리를 사용하는 것이죠.
2. Feed-Forward network의 dimension은 보통 model의 dimension보다 크게 잡습니다. (예를 들어, d_model = 1024일 때 d_ff = 4096정도로 잡습니다.) 따라서 Feed-Forward Network 자체에서 잡히는 메모리 O(d_ff * d_model)역시 모델의 메모리에 큰 영향을 줄 수 있습니다.
3. Self-attention을 계산할 때, input sequence의 길이가 L일 때 time & space complexity는 O(L^2)입니다. Softmax안에 들어가는 행렬 QK^T를 계산해야 하기 때문입니다. 길이가 64000정도 되는 경우에는 batch size를 1로 잡는다고 해도 32bit 실수 64000 * 64000개를 저장하기 위해서는 16GB의 메모리가 필요합니다.
그렇다면 이러한 문제점들을 어떻게 해결할까요? 저자들은 각 문제점들에 대해 다음의 방법들을 제안합니다.
1. Reversible Layer
2. Chunking of Feed-Forward Network
3. Locality-Sensitive Hashing for Self-Attention
이제 각각이 무엇인지에 대해서 하나씩 천천히 알아보도록 합시다.
1. Reversible Layer
앞에서 말했듯이, Transformer의 총 메모리는 layer 숫자에 비례해서 증가하고, 이는 backprop을 위해서 모든 layer의 activation을 저장해야 하기 때문입니다. 만약, 우리가 마지막 layer의 output을 바탕으로 이전 layer의 activation들을 역으로 계산해낼 수 있다면, (시간은 조금 더 걸리더라도) 중간 layer의 activation들을 저장할 필요는 없을 것입니다. 기존의 Transformer는 Attention block과 Feed-Forward block에 Layer normalization과 Residual Connection이 합쳐져 있는 형태이기 때문에 불가능합니다. 일반적으로 다음과 같이 Residual connection으로 주어진 network

의 경우 일반적으로 역함수가 존재하지 않고, 존재한다고 해도 직접 구하는게 어려운 경우가 대부분입니다. 이를 약간 바꿔서 output을 이용해 역으로 input을 계산하는 것이 가능하도록 만들어 준 것이 바로 RevNet입니다. RevNet은 input과 output이 pair로 주어지고, 2개의 network block을 사용하는데, input이 X_1, X_2이고 두 network block F, G가 주어져 있을 때 output Y_1, Y_2는

으로 정의합니다. 기존의 ResNet과 비슷하지만 다른 형태를 띄고 있는데, RevNet의 가장 큰 특징은 역함수가 존재한다는 것 입니다. Y_1, Y_2를 알고 있으면 역으로 X_1, X_2를

로 계산할 수 있기 때문입니다.
Reformer는 RevNet의 아이디어를 그대로 Transformer의 Self-Attention과 Feed-Forward Network에 적용합니다. 그래서 기존의 Network

를
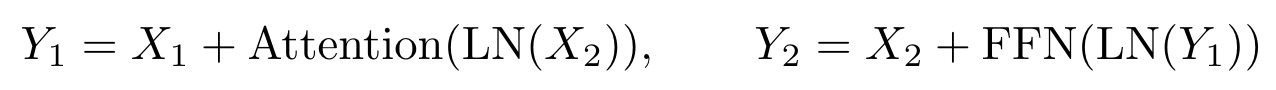
으로 바꾸어서 layer마다 activation을 저장할 필요가 없도록 합니다. 여기서 주의할 점은 논문에서는 input과 output이 pair로 나오는걸 기존의 Transformer처럼 하나의 input과 하나의 output으로 어떻게 바꾸는지 설명되어 있지 않은데, Official Github의 코드를 뜯어보면 아마 X_1 = X_2 = X로, Y = (Y_1 + Y_2)/2로 두는 것으로 추측됩니다. Reformer는 Google이 새로 개발하고 있는 딥러닝 라이브러리인 Trax의 첫번째 실험체로 보이는데, 그 때문에 코드를 이해하는 것이 쉽지 않습니다. (또한, Github에 3개정도의 PyTorch기반의 Reformer implementation이 있는데 그중 두개의 구현이 이 부분을 다르게 구현해 놓았고 이 둘 모두 제가 추측하고 있는 Official implementation과 다른 것으로 보입니다...ㅠ)
2. Chunking of Feed-Forward Network
Feed-Forward Network의 특징은 pointwise, 즉 input sequence의 각 vector에 대한 output이 sequence내의 다른 input에 의존하지 않는 다는 것입니다. 다시 말해서, L개의 input X_1, ..., X_L에 대해서 FFN(X_1), ..., FFN(X_L)을 하나씩 계산하는 것과 하나의 행렬 X = (X_1, ..., X_L)로 만들어 한번에 FFN(X)를 계산하는 것과 결과가 동일합니다. 행렬 연산이 효율적으로 구현되어있다면 후자처럼 구하는 것이 하나씩 따로 계산하는 것 보다 속도는 훨씬 빠르겠지만, 메모리면에서는 전자의 경우 각 계산에 대해서만 들고 있으면 되기 때문에 후자에 비해서 1/L로 줄어들게 됩니다. 둘 사이의 균형을 적절히 맞추기 위해서 논문에서는 L개의 input을 c개의 chunk로 나누어서 한번에 한 chunk씩 계산을 하면서 메모리를 1/c로 줄이게 됩니다. (물론 시간은 조금 더 걸릴 수 있습니다. 시간복잡도는 동일하지만요.) 논문에서는 c=128로 고정된 값을 이용한다고 말합니다.
3. Locality-Sensitive Hashing for Self-Attention
어떻게 보면 이 논문의 핵심이라고 할 수 있는 부분입니다. O(L^2)이 소요되는 Self-Attention의 메모리를 줄이는 한가지 단순한 방법은 앞의 Feed-Forward Network에서 했던 것처럼 모든 query에 대한 Attention을 한번에 계산하지 않고, 한번에 한 query씩 계산하면 memory가 O(L)로 줄어들게 됩니다. 하지만 시간복잡도는 그대로일뿐더러 실제로 계산에 소요되는 시간은 더 걸리므로 문제가 생깁니다. 이를 해결하기 이전에, Attention의 식을 다시 한번 살펴봅시다.
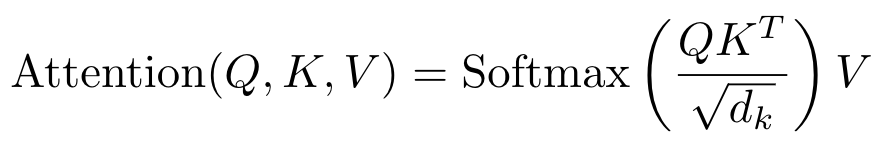
여기서 Attention weight의 계산에 사용되는 Softmax함수가 가지고 있는 성질이 하나 있습니다. 바로 큰 값에 의해서 결과값이 dominate된다는 것이죠. 예를 들어서, (3, 1, 0.5)라는 벡터의 Softmax값을 계산하면 (0.8214, 0.1112,0.0674)가 되는데, input에서의 가장 큰 값인 3에 대한 output의 비중이 다른 input entry의 output에 비해서 훨씬 큰 것을 알 수 있습니다. Transformer의 경우에는, 설령 sequence size가 64000이나 되는 input을 사용한다고 하더라도 주어진 query에 대한 output을 계산하는 데에 있어서 중요하게 여겨지는 key는 얼마 없다고 가정할 수도 있습니다. 그래서 만약, 주어진 query vector에 대해서 inner product값이 큰, 다시 말해서 주어진 query vector와 가까운 key vector를 (예를 들어서) 32개 정도만 잡아서 해당 key에 대해서만 dot-product attention을 계산할 수 있다면 time & space complexity를 모두 줄일 수 있게 됩니다.
이때 가까운 key를 찾는 방법으로 가장 먼저 떠오르는 것은 k-nearest neighborhood를 이용하는 것인데요, 아쉽게도 이는 시간이 너무 오래 걸리기 때문에 좋은 방법이 아닙니다. 그 대안으로 제안하는 것이 바로 Locality-Sensitive Hashing이고, 이를 한문장으로 요약하면 가까이 있는 두 벡터에 같은 hash값을 부여하는 효율적인 방법이라고 할 수 있습니다.
논문에서 사용한 LSH방법은 다음과 같습니다. 총 hash value의 갯수를 b개로 두고, 주어진 query 혹은 key vector x에 대해서 해당 vector의 hash value를

로 정의합니다. 여기서 ;는 두 vector의 concat을 의미하고, d by b/2 matrix인 R은 랜덤하게 생성된 행렬로, 논문에는 나와있지 않지만 Openreview에 적혀있는 저자들의 comment에 따르면 행렬의 각 entry를 정규분포에서 샘플한것으로 보입니다. 예를 들어서, b=4인 경우 행렬 R을 곱하는 것은 d차원 vector를 2차원으로 보내는 것이고, 이 결과가 평면 R^2의 어디에 위치하냐에 따라서 아래 그림과 같이 해쉬값이 결정됩니다.

이렇게 각 query, key vector마다 hash value를 부여한 뒤, 각 query에 대해서 같은 hash값을 가지는 key만 고려합니다. 다시 말해서, i번째 query q_i에 대해서 h(q_i) = h(k_j)인 key k_j들을 찾고, 해당 key들만 q_i에 attend하는 것 입니다. 논문에서는 hash값이 같은 query, key들을 모아놓은 것을 bucket이라고 부르고, 총 hash가 b개이므로 전체 bucket의 수 역시 b개가 됩니다. 이렇게 되면 시간복잡도가 O(L^2)에서 평균적으로

이 되고, bucket size가 상수가 되도록 b를 적당히 크게 잡아주게 되면 Self-Attention의 시간복잡도가 O(L)로 줄어든다고 볼 수 있습니다.
여기서 주의할 점이 있는데, 논문에서는 O(L)이 아닌 O(L log L)이라고 써있고, 사실 이마저도 왜 L log L이 튀어나오는지에 대해서는 설명하고 있지 않습니다. 사실, 위의 계산에는 hash value 자체를 계산하는, 즉 행렬 R을 곱하는 cost에 대해서는 빠져있는데, 실제로 이를 고려하게 되면 총 시간 복잡도가 O(L^2 / b + bL)이 되기 때문에 b = sqrt(L)로 잡으면 O(l^1.5)로 minimize가 되고, 이는 논문에서 이야기한 O(L log L)에 비해서는 큰 값입니다. 실제로 이에 대한 질문을 Openreview에 어떤 분이 남겨놓았는데, 그에 대한 저자들의 답변을 옮겨적자면 다음과 같습니다.
논문에서 언급한대로 b를 L/b가 상수가 되도록 잡게 되면 hash를 계산하는 time complexity O(bL)이 Self-Attention을 계산하는 complexity에 비해서 훨씬 더 커지게 됩니다. 여기서 약간의 트릭을 쓰면, 하나의 random matrix R대신 두개의 d by sqrt(b)/2 random matrix R_1, R_2 를 생성한 뒤, 새로운 hash를 두 random matrix로 얻어지는 hash의 pair, 즉

로 두면 기존과 마찬가지로 b = sqrt(b) * sqrt(b)개의 hash value를 얻지만, 시간복잡도는 O(bL)에서 O(2sqrt(b)L)로 줄어들게 됩니다. 이렇게 되면 이론적으로는 총 시간복잡도 O(L^2 / b + 2sqrt(b)L)를 b = L^1.5일 때 O(L^(4/3))으로 minimize할 수 있습니다. 저자들은 위와 같이 2개의 random matrix를 사용하면 사실상 hash value를 얻는데 들어가는 time cost는 Self-Attention계산에 비해서 무시할 정도이기 때문에 practical하게는 O(L)로 봐도 된다고 합니다. 사실 위와 같이 2개의 random matrix를 사용하는 작업을 당연히 3개 혹은 p개를 사용해서 할 수도 있고, optimal하게는 p = log L정도로 쪼갰을 때 총 시간복잡도가 O(L log L)로 minimize가 됩니다. (Openreview에서 설명한 O(L log L)이 되는 이유는 여기서 설명한 이유와 조금 다르긴 한데, 본질적으로는 똑같습니다.)
다시 본론으로 돌아가서, 여기까지만 하면 문제가 있습니다. 각 bucket의 크기는 일반적으로 다르기 때문에 parellel하게 계산할 수 없다는 점 입니다. 또한, 특정 query에 대해서는 아무런 key도 attend하지 않는 상황이 벌어질 수도 있습니다. 먼저, 두번째 문제는 query와 key를 동일하게 둬서 해결할 수 있습니다. 다시 말해서, query, key embedding weight W_Q, W_K를 하나의 행렬로 두는 것이죠. 이를 Shared-QK라고 부르는데, 실제로 이렇게 설정하는 것이 모델의 성능에 크게 영향을 주지 않는다는 것을 실험에서 보입니다. 이렇게 되면 각 query에 적어도 하나의 key (자기 자신)은 들어가게 됩니다.
또한, parallel한 계산을 위해서 (다시 한번) chunking을 도입합니다. 먼저, 주어진 sequence의 hash value들을 계산한 뒤, 이 값에 따라서 정렬을 합니다. 그 다음에, 정렬된 sequence를 일정한 chunk 크기로 쪼갠 뒤, 각 query에 대해서
1. 같은 chunk, 같은 bucket내의 key
2. 바로 이전 chunk, 같은 bucket내의 key
만 attend를 합니다. 여기서 chunk의 크기는 평균 bucket 크기의 두배, 즉 \(2l/b\)로 잡고, bucket의 크기가 이를 넘어가는 경우, 즉 한 chunk안에 담기지 못하는 경우는 드물다고 주장합니다. 이렇게 chunk로 쪼개게 되면 parallel하게 계산할 수 있고 원하던 time complexity를 얻게 됩니다.
만약 bucket size가 너무 작다면 어떡할까요? 다시 말해서, 주어진 query에 대해서 attend하는 key의 숫자가 1~2개밖에 되지 않는다면, 이 역시 문제가 될 수 있습니다. (attend해야 마땅할 key가 LSH를 통해서 걸러져 버리는 것이죠.) 이는 단순하게 LSH를 여러번 하는 것으로 해결할 수 있습니다. 예를 들어서, random matrix를 n_r번 생성해서 hash를 n_r번 계산한 뒤, 한번이라도 같은 hash value를 가지면 같은 bucket에 포함시키면 됩니다. (논문에서는 여러 값에 대해서 실험을 하긴 하지만 n_r = 8이 가장 성능 면에서 좋은 것으로 나타납니다.)
또 한가지 주의할 점은, shared-QK 셋팅에서는 자기 자신이 무조건 같은 bucket에 들어가기 때문에 무조건 attend를 하게 된다는 것 입니다. 하지만, 이게 원하는 상황은 아니기 때문에 (Illustrated Transformer에서도 볼 수 있듯이 꼭 자기 자신의 attention값이 클 이유는 없고 보통은 그렇지 않습니다) 이를 방지하기 위해서 subsequent masking을 하는 것 처럼 Softmax를 계산하기 전에 QK^T 행렬에서 대각 성분은 10^5씩 빼 줍니다. 물론 bucket하나에 하나의 query, key만 들어가는 경우, 혹은 decoder의 masked Self-Attention에서 첫번째 token인 경우에는 어쩔 수 없이 자기 자신만 attend를 할 수 밖에 없는데, 위의 process는 이를 다 고려한다고 봐도 됩니다.
Encoder-Decoder Attention의 경우에는 LSH를 어떻게 적용해야 할까요? 앞에서 말한 shared-QK는 Machine Translation같이 Encoder와 Decoder를 모두 사용하는 경우에는 쓸 수 없습니다. 아쉽게도, 논문에서는 이에 대해서 언급하지 않고 있고, 다시 Openreview로 가보면 shared-QK가 꼭 필요하다고 하고 있기 때문에 이에 대한 연구가 더 필요할 것으로 보입니다.

실험의 경우 총 4가지를 진행하였습니다. 먼저, 논문 중간에 등장하는 Synthetic task는 반복되는 문자열의 앞부분을 바탕으로 뒷부분을 예측하는 task로, LSH Attention의 성능을 보기 위한 실험입니다. 이 task에서 총 sequence 길이를 1024로 길게 잡았기 때문에 span이 작은, 예를 들어서 특정 query에 대해서 앞의 256개 정도의 key만 attend하는 Transformer로는 풀 수 없는 task라고 할 수 있습니다. 아래 표에서 볼 수 있듯이, LSH Attention을 사용하는 것이 performance에 거의 영향을 주지 않습니다.

그 다음은 enwik8-64K와 imagenet-64에 대한 실험인데, imagenet-64는 하나의 이미지를 길이 \(3 * 64* 64 = 12288\)의 sequence로 봐서 image generation task를 수행했습니다. 둘다 bits per dimension이라는 metric으로 성능을 측정했는데, 이는 단순히 NLL loss를 dimension으로 나누어준 값으로 보면 됩니다. 아래의 그래프들은 shared-QK를 사용하는 것과 Reversible Transformer를 사용하는것이 성능에 영향을 거의 주지 않는 것을 보여줍니다.

LSH Attention에 대해서도 성능 측정을 했는데요, round의 숫자를 늘릴수록 full attention의 성능에 근접하고, n_r = 8정도만 되어도 full-attention과 별 차이 없는 성능을 보여줍니다. 하지만, Figure 5의 오른쪽 그래프가 보여주듯이 training에 걸리는 시간은 n_r에만 비례할 뿐 full-attention에 비해서는 훨씬 적게 걸립니다. (이 그래프는 enwik8이나 imagenet이 아닌 처음에 언급한 synthetic task에 대한 결과입니다.)
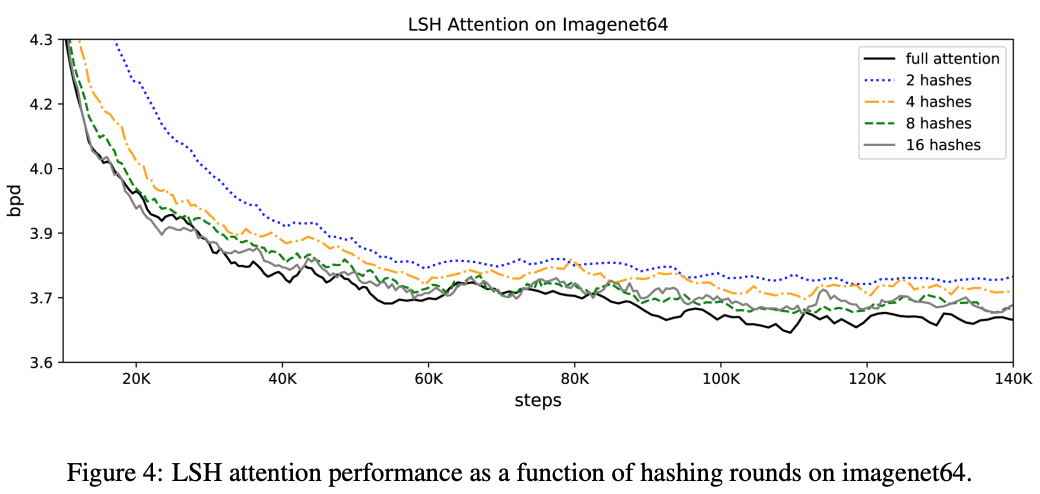

마지막으로, Machine Translation에 대해서도 BLEU score를 통해서 성능을 측정하였는데, 이 경우에는 sequence 길이(문장 내 단어수)가 대부분 128을 넘지 않기 때문에 LSH attention을 사용하지 않고 Reversible Transformer에 대해서만 성능을 보았다고 합니다. (Encoder-Decoder LSH attention을 못하기 때문인 것 같기도 하지만...) 결과는 Reversible Transformer를 사용하는 것이 성능을 크게 떨어뜨리지 않는다고 합니다.

정리하자면, 저자들은 LSH attention, Reviersible Transformer, Chunking등을 이용해서 기존 Transformer에 비해서 time & memory efficient한 Reformer를 제안하였고, image generation이나 Machine Translation같은 실험을 통해서 모델의 타당성을 보였습니다. Music generation이나 time-series forcasting에 대해서도 언급하고 있는데 이런 Task들에 Reformer를 적용해 보는것도 좋은 후속 연구로 보입니다.
'Machine Learning & Deep Learning > Natural Language Processing' 카테고리의 다른 글
| Extract Training Data from Large Language Models (0) | 2021.01.11 |
|---|---|
| F^2-Softmax: Diversifying Neural Text Generation via Frequency Factorized Softmax (0) | 2020.12.14 |
| Data Augmentation in Natural Language Processing (0) | 2020.07.11 |
| Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention (0) | 2020.07.05 |
| Synthesizer: Rethinking Self-Attention in Transformer Models (4) | 2020.05.09 |




